Più di un mese fa avevo sollevato la questione su come trovare un metodo per stabilire un punto interno ad un poligono qualsiasi. La questione era stata posta in questo articolo, anche se più di qualcuno aveva confuso questo tipo di problema col problema di stabilire se un punto si trovi o meno dentro un poligono.
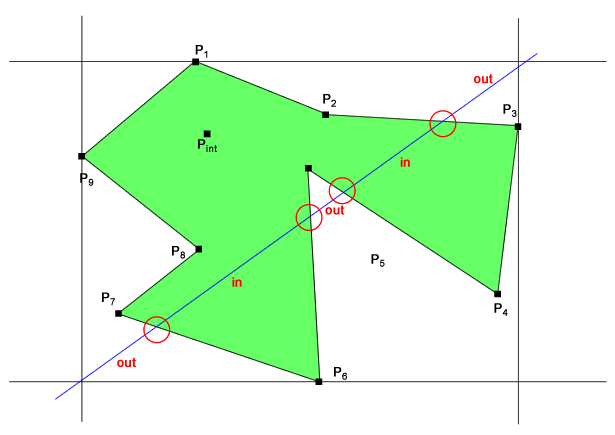
Ripeto ancora una volta la questione: il problema algoritmico è proprio quello di trovare un punto completamente contenuto in un poligono ed il poligono può essere indifferentemente convesso o concavo. Il punto deve trovarsi internamente e non sul bordo, altrimenti basterebbe prendere uno qualsiasi dei vertici del perimetro o il punto medio di un qualsiasi lato.
La soluzione più elegante ed al tempo stesso molto pratica da implementare algoritmicamente si basa sul fatto che qualsiasi poligono è sempre suddivisibile in triangoli e, grazie a questa cosa, si può dimostrare per induzione che una soluzione valida al problema è il punto medio di una diagonale del poligono. E' chiaro che a questo punto la parte "difficile" è trovare una diagonale "interna" al poligono, cioè un segmento che congiunge una coppia qualsiasi di lati. Probabilmente in un poligono possono essere tante le diagonali completamente contenute nel poligono, ma ci limiteremo a trovare la prima.
Supponiamo per un attimo di pensare ad un algoritmo molto semplice per pervenire a soluzione:
- ciclare da 1 ad n per costruire preventivamente l'insieme dei lati del poligono
- prendere ad uno ad uno ogni vertice (i) da 1 fino a n, se n è il numero di vertici del poligono
- prendere ad uno ad uno un altro vertice (j) da i+1 fino ad n, con cui andare a formare una diagonale di prova, che non deve appartenere all'insieme dei lati del poligono
- prendere ad uno ad uno uno lato k nell'insieme dei lati costituenti il poligono
- controllare se la diagonale di prova che congiunge il vertice i al vertice j interseca il lato k
- se la diagonale di prova non interseca alcun altro lato, essa potrebbe essere completamente contenuta nel poligono, come potrebbe anche essere completamente esterna al poligono
- controllare se il punto medio della diagonale di prova è dentro o fuori il poligono e se è dentro, abbiamo la soluzione al problema
Come potete vedere questa implementazione è relativamente semplice, ma tutto fuorché efficiente, visto che la sua complessità polinomiale è O(n3).
Arriviamo pertanto al dunque, cioè illustro rapidamente il metodo che è basato sulla dimostrazione che esiste sempre una diagonale interna in un poligono [O'Rourke 13-14]. L'idea è appunto che il punto medio di una diagonale interna è sicuramente interno al poligono.
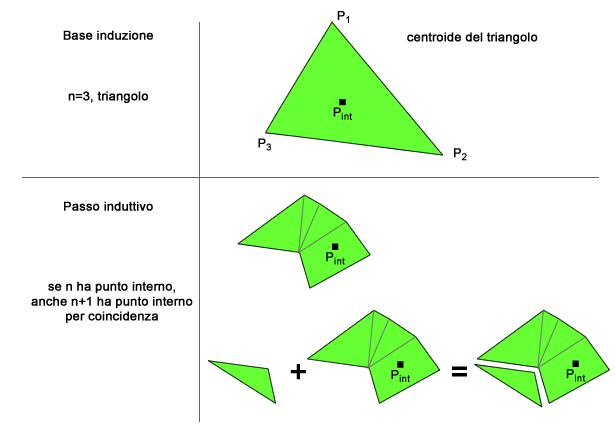
La dimostrazione per induzione la possiamo fare considerando il numero di vertici/lati di un poligono. Se c'è la soluzione per un poligono di N lati, si può trovare anche la soluzione per un poligono di N+1 lati.
Nel caso del triangolo, base dell'induzione perché è il poligono con numero minimo di lati (3), la soluzione al problema la troviamo banalmente utilizzando il centroide tra i tre vertici.
Per un quadrilatero, se esso è convesso, abbiamo due diagonali interne, quindi sicuramente entrambe vanno bene, se invece il quadrilatero è concavo, abbiamo una sola diagonale interna, ma abbiamo comunque la soluzione. C'è da notare che una diagonale interna è proprio il lato che è condiviso tra due triangoli contigui di una possibile triangolarizzazione di un poligono, cioè basta considerare in una triangolarizzazione proprio uno dei lati contigui dei triangoli come diagonale interna.
Passiamo ora all'algoritmo:
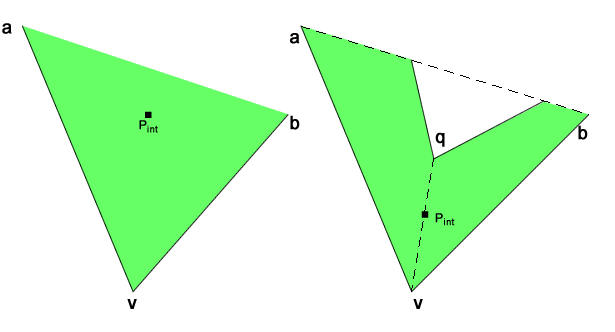
- individuare un vertice convesso v del poligono e consideriamo a e b i vertici adiacenti a v
- per ogni altro vertice q del poligono:
- se il vertice q è dentro il triangolo avb, calcolare la distanza di v ortogonale al segmento ab
- tenere per buono il vertice q se la sua distanza è minima rispetto alle altre calcolate
- se non esiste alcun punto q dentro il triangolo avb, allora considerare come soluzione il punto medio del segmento ab o il centroide di avb
- se invece qualche punto q è dentro il triangolo avb, allora la diagonale qv è sicuramente interna ed in tal caso la soluzione è il suo punto medio
Nell'immagine qui a lato potete notare che il punto più vicino alla retta ab, non cade dentro al triangolo avb, quindi la soluzione al problema è proprio data dal centroide del triangolo avb o il punto medio del segmento ab, in quanto diagonale interna.
Potete notare che la complessità dell'algoritmo è O(n), quindi non si può desiderare niente di meglio dal metodo: esso è ottimale anche come performance.