Some months ago I challenged my readers to find a method to determine an inner point inside a polygon. I described the original issue in this article in Italian language, altough more than one lector confused this issue with another one, i.e. determine if a point is inside or not in a polygon.

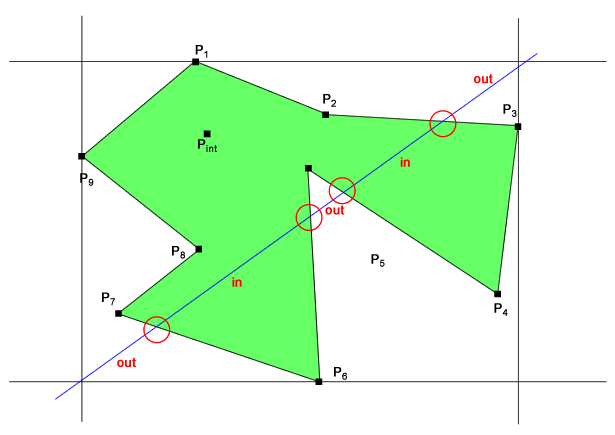
I would spend a little bit more on the issue: the algorytmic problem is to find a point completely inside the polygon, whatever the polygon is convex or concave. The satisfying point must lay completely in the inner region bounded by the polygon, not over the bound, otherwise you could solve the problem taking any of the vertexes or the mid point over any edge.

The most elegant solution I found - which is also very effective to outfit in programming code - is based on the fact tha any polygon may be always discretized in triangles and you may prove for induction that a valid solution is a mid point taken over and inner diagonal of the polygon. What's difficult is finding an inner diagonal, i.e. a segment that connects any pair of vertexes. In each polygon you can find several diagonals completely inside the polygon, but you can stop as soon as you find the first one.

Let's make a proposal for an easy algorytm to get some solution:

• loop from 1 to n over the set of the polygon vertexes
• take the i-th vertex from 1 to n, if n is the amount of the polygon vertexes
  • take another j-th vertex where j loops from i+1 to n and let's trace the test diagonal, which doesn't have to belong to the edges set
    • take each k-th edge in the edges set
      • check if the test diagonal from i to j intersects k-th edge
    • if the test diagonal doesn't intersect any edge, it could be completely embraced in the polygon or it could be completely outside the polygon
    • check if the mid point of the test diagonal is inside or outside the polygon if the mid point is inside, return it as the solution

As you may see, this pseudocode is quite easy to understand, although it is far from being efficient: its polynomial complexity is O(n³).

Let's go a step further and let's quickly see the method based on the proof that an inner diagonal always exists inside a polygon [O'Rourke 13-14]. The idea behind is that the mid point of the inner diagonal is always inside the polygon.

You may prove that for induction using the amount of vertexes and sides of the polygon. If you find a solution for an N-vertexes polygon, you can find a solution even for an N+1-vertexes polygon.

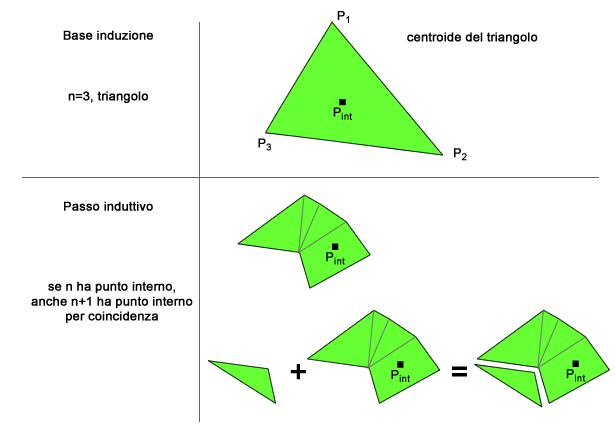
The base of induction is the easiest polygon, the triangle. In the triangle the solution to the problem is trivial: just use the centroid of the vertexes.

For a quadrangle, if it is convex, you get two inner diagonals and both satisfy the algorytm choice. If the quadrangle is concave, only one diagonal is completely inside, but the solution is whatsoever found. You can notice that the inner diagonal is the side shared between two adjacent triangles got by the triangular meshing of the polygon, so you just need to consider any shared side of two triangles in the mesh.

Let's move to the inductive step:

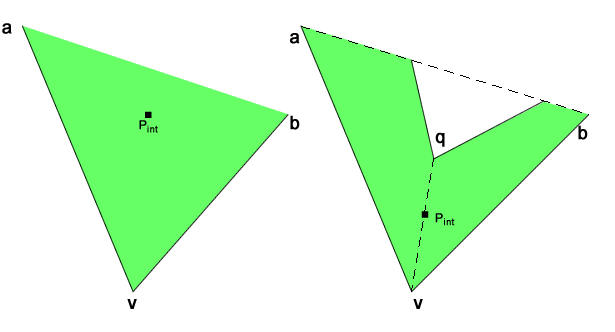
• find a convex vertex v in the polygon and consider a and b as adjacent vertexes surrounding v
• for each other vertex q in the polygon
  • if the vertex q is inside the triangle avb, calculate the distance of v to the segment ab
  • keep vertex q as solution if its distance is minimal with respect other found vertexes
• if no vertexes q have been found inside avb, use the mid point of segment ab as solution or the centroid of triangle avb
• if some vertex q is inside the triangle avb then the diagonal qv is surely inside and the solution is its mid point

In the image shown above, you may noticed that the nearest point to segment ab, doesn't lay in triangle avb, so the solution in the centroid in triangle avb or the mid point of segment ab, which is an inner diagonal.

You may notice that algorytm complexity is O(n), which is the best you would ask for: its optimal even in the performance space.