Domenica scorsa si sono visti a Locara parecchi concorrenti non tirarsi indietro alla sfida nella sfida, cioè quella di correre in gara contro gli altri concorrenti - andava in scena la quinta edizione del Trofeo San Valentino organizzato dal Team Ciclotazze - ma soprattutto quella non meno ardua di cimentarsi contro il freddo polare e la consistente precipitazione nevosa.

Sicuramente concorrenti portoghesi non se ne sono visti, se non qualche ciclista di appoggio all'organizzazione: tutti hanno preferito assistere a bordo strada, come il sottoscritto armato di fotocamera, o starsene saggiamente a casa.

Incurante delle intemperie, c'era però un "animale" alquanto insolito - per il look invernale Focus 2012, guanti e casco giallo fluò - che è partito con minimo vantaggio sulla testa della gara ed ha provato a resistere fino alla fine: sfilato a pochi chilometri dall'arrivo, il "Biondo", al secolo Davide Biondani, dal 2012 in forza al Team Focus Italia, se ne è partito da casa per raggiungere Locara, si è fatto tutti i 47 km del percorso di gara e poi se ne sarà sicuramente tornato a casa, per la bellezza di "soli" 85 km, stando a conti che ho fatto per conto mio.

Una domanda sorge spontanea: ma ci te l'ha fato far, Biondo?

Sabato mattina, causa addormentamento, ho ignorato completamente la sveglia delle 8.00, quella che avrebbe dovuto farmi trovare alla rotonda di Montorio all'appuntamento "Pedala col Conte", ma me la son presa con comodo, facendo colazione con Elisa ed i miei figli più piccoli e astenendomi volentieri dal congelamento per il trasferimento verso la cittadina ad est di Verona.

La voglia però di andare in MTB era intatta e, visto che il cielo non prometteva niente di buono con i primi fiocchi che si apprestavano a cadere a Grezzana, con un paio di SMS facevo cadere la maggioranza del Trio Piocio e mi accordavo con l'Orlando per un giro alternativo a quello del savoiardo.

Dopo venti minuti, lo zio Paolo era a casa mia armato della sua Rockrider 8XC in configurazione "all mountain" e guanti a doppio strato, per allontanare per quanto possibile i ghiaccioli ed il freddo buriano.

Salutata la mia famigliuola, si parte per il nostro giro e Paolo fa subito sapere che sarà un "giro riscaldante", cioè basse, bassissime velocità, ma caldo, sudore e frequenze cardiache belle alte.

E' così che attacchiamo una salita per me inedita, aperta da non molto stando alle parole di Paolo, cioè quella che sale dalle grotte degli Americani verso Slaìn, il cui inizio è collocato si e no duecento metri più a sud della ben più nota discesa omonima.

Lo strato di neve è già di cinque centimetri, ma il grip è ottimo e si sale subito di buona lena e con un livello cardiaco alto. Il BB King posteriore da 26" del Paolo stenta un paio di volte sulle pendenze più accentuate, mentre il gommone da 29x2,25 della Scalona non batte ciglio, se non fosse che il mio tiro è quello che è e dove Paolo invece riesce a passare indenne, io son costretto a spingere a piedi per "fiato esaurito".

In un breve lasso di tempo ci ritroviamo già attorno alla casa di Slaìn e proseguiamo spediti verso Campo Piano, dove abbandoniamo il bosco in favore dell'asfalto della provinciale che congiunge Grezzana a Montecchio. Da lì in poi tutto secondo manuale, cioè saliamo al Capitello San Vincenzo, segue la cresta single track dei Casotti e poi giù in discesa verso Salvalaio in tutta sicurezza. Ad Alcenago saliamo fino a Vigo per scegliere il bellissimo single track della Ria, da qui al Capitello San Giuseppe e poi a casa dei miei genitori per una breve pausa a base di grappa alla ruta e ginepro, mentre fuori i fiocchi cadono insistentemente.

Dopo aver riscaldato gli animi con lo spirito, ritorniamo in piazza alla Chiesa per affrontare la parte finale di una discesa dell'edizione 2010 della Verona-Boscochiesanuova, ossia il tratto dal Capitello San Giuseppe a Bosemai. Peccato che la discesa sterrata finisca presto: ci congeliamo per percorrere quel paio di chilometri che ci servono per arrivare in Turnover dove fare il punto della situazione.

Pochissimi chilometri pertanto lo scorso weekend, nemmeno sedici, e poco più di un'ora in sella alla bici, però la tecnica sia in salita che in discesa non è mancata, così come anche il divertimento: quando c'è la neve, è sempre garantito. Speriamo che si riesca nel prossimo weekend a pedalare molto di più in sella alle nostre mountain bike.

Più di un mese fa avevo sollevato la questione su come trovare un metodo per stabilire un punto interno ad un poligono qualsiasi. La questione era stata posta in questo articolo, anche se più di qualcuno aveva confuso questo tipo di problema col problema di stabilire se un punto si trovi o meno dentro un poligono.

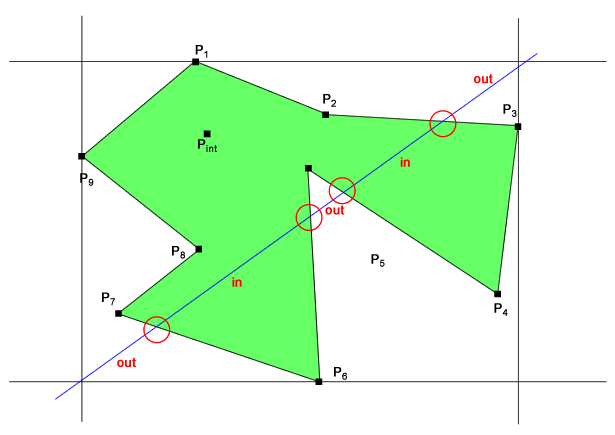
Ripeto ancora una volta la questione: il problema algoritmico è proprio quello di trovare un punto completamente contenuto in un poligono ed il poligono può essere indifferentemente convesso o concavo. Il punto deve trovarsi internamente e non sul bordo, altrimenti basterebbe prendere uno qualsiasi dei vertici del perimetro o il punto medio di un qualsiasi lato.

La soluzione più elegante ed al tempo stesso molto pratica da implementare algoritmicamente si basa sul fatto che qualsiasi poligono è sempre suddivisibile in triangoli e, grazie a questa cosa, si può dimostrare per induzione che una soluzione valida al problema è il punto medio di una diagonale del poligono. E' chiaro che a questo punto la parte "difficile" è trovare una diagonale "interna" al poligono, cioè un segmento che congiunge una coppia qualsiasi di lati. Probabilmente in un poligono possono essere tante le diagonali completamente contenute nel poligono, ma ci limiteremo a trovare la prima.

Supponiamo per un attimo di pensare ad un algoritmo molto semplice per pervenire a soluzione:

• ciclare da 1 ad n per costruire preventivamente l'insieme dei lati del poligono
• prendere ad uno ad uno ogni vertice (i) da 1 fino a n, se n è il numero di vertici del poligono
  • prendere ad uno ad uno un altro vertice (j) da i+1 fino ad n, con cui andare a formare una diagonale di prova, che non deve appartenere all'insieme dei lati del poligono
    • prendere ad uno ad uno uno lato k nell'insieme dei lati costituenti il poligono
      • controllare se la diagonale di prova che congiunge il vertice i al vertice j interseca il lato k
    • se la diagonale di prova non interseca alcun altro lato, essa potrebbe essere completamente contenuta nel poligono, come potrebbe anche essere completamente esterna al poligono
    • controllare se il punto medio della diagonale di prova è dentro o fuori il poligono e se è dentro, abbiamo la soluzione al problema

Come potete vedere questa implementazione è relativamente semplice, ma tutto fuorché efficiente, visto che la sua complessità polinomiale è O(n³).

Arriviamo pertanto al dunque, cioè illustro rapidamente il metodo che è basato sulla dimostrazione che esiste sempre una diagonale interna in un poligono [O'Rourke 13-14]. L'idea è appunto che il punto medio di una diagonale interna è sicuramente interno al poligono.

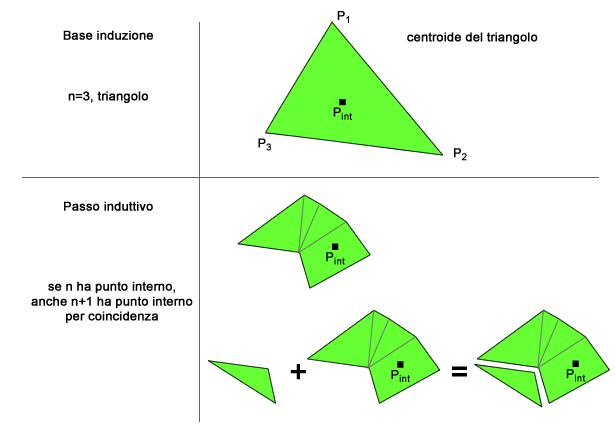
La dimostrazione per induzione la possiamo fare considerando il numero di vertici/lati di un poligono. Se c'è la soluzione per un poligono di N lati, si può trovare anche la soluzione per un poligono di N+1 lati.

Nel caso del triangolo, base dell'induzione perché è il poligono con numero minimo di lati (3), la soluzione al problema la troviamo banalmente utilizzando il centroide tra i tre vertici.

Per un quadrilatero, se esso è convesso, abbiamo due diagonali interne, quindi sicuramente entrambe vanno bene, se invece il quadrilatero è concavo, abbiamo una sola diagonale interna, ma abbiamo comunque la soluzione. C'è da notare che una diagonale interna è proprio il lato che è condiviso tra due triangoli contigui di una possibile triangolarizzazione di un poligono, cioè basta considerare in una triangolarizzazione proprio uno dei lati contigui dei triangoli come diagonale interna.

Passiamo ora all'algoritmo:

• individuare un vertice convesso v del poligono e consideriamo a e b i vertici adiacenti a v
• per ogni altro vertice q del poligono:
  • se il vertice q è dentro il triangolo avb, calcolare la distanza di v ortogonale al segmento ab
  • tenere per buono il vertice q se la sua distanza è minima rispetto alle altre calcolate
• se non esiste alcun punto q dentro il triangolo avb, allora considerare come soluzione il punto medio del segmento ab o il centroide di avb
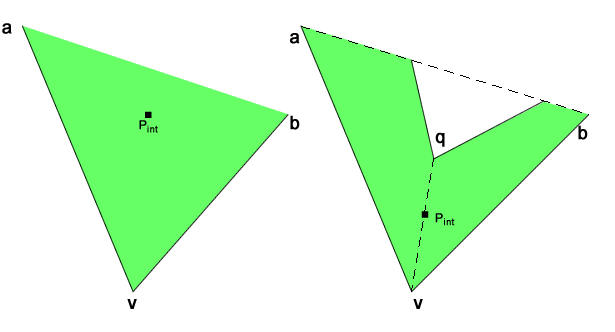
• se invece qualche punto q è dentro il triangolo avb, allora la diagonale qv è sicuramente interna ed in tal caso la soluzione è il suo punto medio

Nell'immagine qui a lato potete notare che il punto più vicino alla retta ab, non cade dentro al triangolo avb, quindi la soluzione al problema è proprio data dal centroide del triangolo avb o il punto medio del segmento ab, in quanto diagonale interna.

Potete notare che la complessità dell'algoritmo è O(n), quindi non si può desiderare niente di meglio dal metodo: esso è ottimale anche come performance.